vendredi 15 mai 2015
samedi 28 février 2015
mercredi 18 février 2015
L'exposé
Voici des documents pouvant vous aider pour organiser votre travail et voir un peu plus ce que j'attend de vous.
http://www.intellego.fr/intelleblog/methode-pour-faire-et-presenter-un-expose-ou-une-soutenance/4521
http://ekladata.com/lutinbazar.eklablog.com/perso/outils%20pour%20la%20classe/expose/fiches%20memo%20expose_preparer.pdf
Voici des documents pour t'aider à créer un PowerPoint.
https://support.office.com/fr-be/article/Cr%C3%A9er-un-mod%C3%A8le-PowerPoint-254a0db6-1311-4a98-b829-e09b5019512b
http://protuts.net/10-etapes-pour-creer-une-presentation-powerpoint-professionnelle/
http://www.intellego.fr/intelleblog/methode-pour-faire-et-presenter-un-expose-ou-une-soutenance/4521
http://ekladata.com/lutinbazar.eklablog.com/perso/outils%20pour%20la%20classe/expose/fiches%20memo%20expose_preparer.pdf
Voici des documents pour t'aider à créer un PowerPoint.
https://support.office.com/fr-be/article/Cr%C3%A9er-un-mod%C3%A8le-PowerPoint-254a0db6-1311-4a98-b829-e09b5019512b
http://protuts.net/10-etapes-pour-creer-une-presentation-powerpoint-professionnelle/
La trigonométrie: les formules
Voici une petite vidéo reprenant les formules de trigonométrie utilisées en 3e année.
https://www.youtube.com/watch?v=amxLRE79pXw
https://www.youtube.com/watch?v=amxLRE79pXw
La trigonométrie
La trigonométrie
Quand on parle de trigonométrie, on associe nécessairement le mot aux fonctions cosinus, vues en 4e, puis sinus et tangente, vues en 3e pour le calcul de longueurs ou d’angles dans le triangle.
Aujourd’hui, l’usage de la calculatrice est incontournable lorsqu’on applique ces fonctions. Mais si l’on remonte à la fin des années 70, les collégiens ne disposaient pas encore de calculatrice et devaient se munir de tables trigonométriques pour effectuer les calculs.
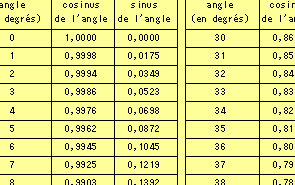
Le mot vient du grec "trigone" (triangle) et "metron" (mesure).
Dans l’Encyclopédie (1751), Jean le Rond d’Alembert (1717 ; 1783) définit la trigonométrie comme « l’art de trouver les parties inconnues d’un triangle par le moyen de celles qu’on connaît ». C’est bien la démarche qui est demandée aux élèves du collège. Et pourtant la trigonométrie n’est pas à l’origine un outil de calcul du triangle mais du cercle.
Il faut remonter jusqu’aux babyloniens, 2000 ans avant notre ère, pour trouver les premières traces de tables de données astronomiques. Car à la base, la trigonométrie est une géométrie appliquée à l’étude du monde, de l’univers et est indissociable de l’astronomie.
L’héritage de ces tables données aux grecs et la numération sexagésimale des babyloniens (base 60) contribuera à l’introduction du partage du cercle en 360°.
Eratosthène de Cyrène (-276 ; -196) et Aristarque de Samos (-310 ; -230) utilisent ces tables pour l’astronomie. Eratosthène se rendra célèbre pour avoir calculé la circonférence de la terre avec une précision tout à fait remarquable (seulement 3% d’erreur).
Mais on attribue à Hipparque de Nicée (-190 ; -120) les premières tables trigonométriques. Elles font correspondre l’angle au centre et la longueur de la corde interceptée dans le cercle.
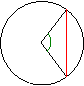
Le grec Claude Ptolémée (90? ; 160?) poursuit dans l’Almageste les travaux d’Hipparque avec une meilleure précision et introduit les premières formules de trigonométrie. Ptolémée croyait au géocentrisme : le terre est le centre de l’univers, tous les astres gravitent autour d’elle. Il faudra attendre le XVIe siècle pour rétablir la vérité pourtant déjà connue de Pythagore de Samos(-569 ; -475) au Ve siècle avant J.C.
 |  |
En Orient, l’indien Aryabhata l'Ancien (476 ; 550) utilise la demi corde et donne les premières tables de sinus. On retrouve la configuration du sinus dans le triangle rectangle telle qu’elle est enseignée aux collégiens aujourd’hui. Aryabhata est le premier à voir la trigonométrie hors du cercle.
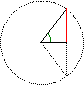
Dès le XIIIe siècle, les arabes, tel que le perse Mohammed al Khwarizmi (780 ; 850) traduisent les ouvrages provenant d’Orient.
Mohammed al Battani (850 ; 929) introduit les tables de tangentes et de nouvelles formules, puis après lui Muhammad Abu'l-Wafa (940 ;998) précise encore ces tables.
Avec le perse al Tusi (1201-1274), la trigonométrie se sépare de l’astronomie.
Mohammed al Battani (850 ; 929) introduit les tables de tangentes et de nouvelles formules, puis après lui Muhammad Abu'l-Wafa (940 ;998) précise encore ces tables.
Avec le perse al Tusi (1201-1274), la trigonométrie se sépare de l’astronomie.
 | Regiomontanus, allemand (1436 ; 1476) |
Plus tard, l’astronome et mathématicien Regiomontanus, de son vrai nom Johann Müller développe la trigonométrie comme une branche indépendante des mathématiques.
Il serait à l’origine de l’usage systématique du terme sinus.
Il serait à l’origine de l’usage systématique du terme sinus.
Au XVIe siècle, le français François Viète (1540 ; 1607), conseiller d’Henri IV, fera évoluer la trigonométrie pour lui donner le caractère qu’on lui connaît aujourd’hui.
De nos jours, la trigonométrie trouve des applications très diverses, particulièrement dans les sciences physiques. La propagation des ondes, par exemple, est transcrite par des fonctions trigonométriques.
Ayons enfin une petite pensée pleine de compassion aux lycéens des classes scientifiques qui voient arriver leurs premiers cheveux blancs avec les nombreuses et redoutables formules de trigonométrie qu’il faut connaître et savoir appliquer.
Pour exemple, en voici quelques-unes :
 |  |
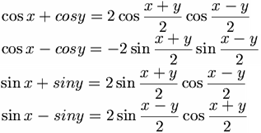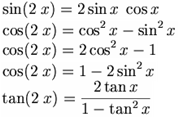Euclide et les triangles isométriques 1
Comme dans tous les domaines, le vocabulaire mathématique a évolué au cours du temps. Ainsi Euclide parlait dans ses Eléments de cas d'égalité de triangles et non de cas d'isométrie.
Avant de parler de ce qu'Euclide a découvert sur les triangles, essayons de découvrir qui il était et quelle est son histoire.
Euclide d'Alexandrie - Grec (-320? ; -260?)
Copie en grec des Eléménts (IXème siècle)
Postulat 1 :
Par deux points distincts, il passe une droite et une seule.
Postulat 2 :
Tout segment est prolongeable en une droite.
Postulat 3 :
Deux points distincts étant donnés,
il passe un cercle et un seul de centre le premier point et passant par le second.
Postulat 4 :
Tous les angles droits sont égaux entre eux.
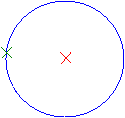
Postulat 5 :
Par un point extérieur à une droite, il passe une droite et une seule parallèle à la droite donnée.
Lobatchevski
Avec le compas, Euclide (vu par Raphaël)
Avant de parler de ce qu'Euclide a découvert sur les triangles, essayons de découvrir qui il était et quelle est son histoire.
Euclide d'Alexandrie - Grec (-320? ; -260?)
Euclide est un des plus grands mathématiciens de l’Antiquité et pourtant on ne connaît pas grand chose de sa vie.
Il aurait commencé ses études dans l’Académie, l’école d’Athènes fondée par Platon. Il y apprend la géométrie d’Eudoxe de Cnide (-408 ; -355) et de Théétète d'Athènes (-415 ; -369).
On sait qu’il vit à Alexandrie en Egypte, ville érigée par Alexandre le Grand en 331 avant J.C. et célèbre pour son phare aujourd'hui détruit.
Dans la prestigieuse Ecole d’Alexandrie, il dirige une équipe de mathématiciens qui participent à l’écriture de son œuvre. Cette école connaîtra plus tard d’autres savants tels qu’Archimède de Syracuse (-287 ; -212) et Apollonius de Perge (-262 ; -190).
Il aurait commencé ses études dans l’Académie, l’école d’Athènes fondée par Platon. Il y apprend la géométrie d’Eudoxe de Cnide (-408 ; -355) et de Théétète d'Athènes (-415 ; -369).
On sait qu’il vit à Alexandrie en Egypte, ville érigée par Alexandre le Grand en 331 avant J.C. et célèbre pour son phare aujourd'hui détruit.
Dans la prestigieuse Ecole d’Alexandrie, il dirige une équipe de mathématiciens qui participent à l’écriture de son œuvre. Cette école connaîtra plus tard d’autres savants tels qu’Archimède de Syracuse (-287 ; -212) et Apollonius de Perge (-262 ; -190).
Copie en grec des Eléménts (IXème siècle)
L’ œuvre phénoménale, « Les éléments », que nous laisse Euclide, servira de base à toute la géométrie pendant plus de 2000 ans. Après la Bible, c'est l'ouvrage qui possède le plus d'éditions. Une vraie encyclopédie, composée de 13 livres, qui traite des figures géométriques, des polygones inscrits et circonscrits à un cercle, des proportions, de la géométrie dans l’espace ainsi que des nombres. Deux autres livres seront complétés plus tard par Archimède (cercles, cylindres, Apollonius (cônes, coniques : ellipse, parabole, hyperbole).
Les premières démonstrations rendent cette œuvre novatrice pour l’époque. Euclide apporte des définitions rigoureuses et démontre les grands théorèmes de ses ancêtres, comme ceux de Thalès de Milet (-624 ; -548) et Pythagore de Samos (-569 ; -475) par exemple.
Dans "Les éléments", on trouve en particulier les cinq postulats qui fondent les bases de la géométrie.
« Postulat » vient du latin « postulare = demander ». Un postulat est un principe que l’on demande d’accepter, qui est admis pour établir une démonstration ou pour la poursuite d’une théorie.
« Postulat » vient du latin « postulare = demander ». Un postulat est un principe que l’on demande d’accepter, qui est admis pour établir une démonstration ou pour la poursuite d’une théorie.
Par deux points distincts, il passe une droite et une seule.
Postulat 2 :
Tout segment est prolongeable en une droite.
Postulat 3 :
Deux points distincts étant donnés,
il passe un cercle et un seul de centre le premier point et passant par le second.
Postulat 4 :
Tous les angles droits sont égaux entre eux.
Postulat 5 :
Par un point extérieur à une droite, il passe une droite et une seule parallèle à la droite donnée.
Ce dernier postulat aussi appelé Postulat d’Euclide est le fondement de la géométrie euclidienne.
Puisqu’il est admis, un mathématicien russe Nicolaï Ivanovitch Lobatchevski (1793 ; 1856), un hongrois János Bolyai (1802-1860) et un allemand Carl Friedrich Gauss (1777-1855) affirmeront sa négation :
Puisqu’il est admis, un mathématicien russe Nicolaï Ivanovitch Lobatchevski (1793 ; 1856), un hongrois János Bolyai (1802-1860) et un allemand Carl Friedrich Gauss (1777-1855) affirmeront sa négation :
« Il existe une infinité de parallèles passant par un point extérieur à une droite donnée. »
Même si cela peut paraître surprenant, ils construisent, comme Euclide une nouvelle géométrie complète et cohérente, la première géométrie non-euclidienne.
Lobatchevski
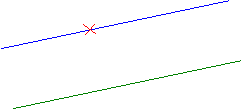
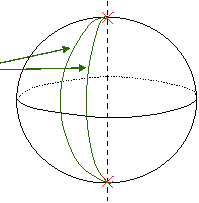
Par la suite, d’autres géométries non euclidiennes seront créées comme la géométrie sphérique de l'Allemand Bernhard Riemann (1826-1866) :
« Il n'existe pas de parallèle passant par un point extérieur à une droite donnée. »
Un exemple "concret" de cette géométrie se trouve par exemple sur la sphère :
« Deux droites quelconques sont sécantes en deux points. (!!!) »
« Deux droites quelconques sont sécantes en deux points. (!!!) »
Dans le livre XIII, Euclide étudie aussi les cinq polyèdres réguliers (dits de Platon). Il démontre qu’il en existe cinq et cinq seulement : le tétraèdre, l'octaèdre, l’icosaèdre, le cube et le dodécaèdre.
(Les faces d’un polyèdre régulier sont des polygones réguliers tous identiques.)
(Les faces d’un polyèdre régulier sont des polygones réguliers tous identiques.)
Les livres VII, VIII et IX parlent d'arithmétique (science des nombres). Euclide travaille en particulier sur les nombres premiers(nombre ayant aucun diviseur autre que 1 et lui-même) et prouve entre autre que leur nombre est infini. Il ne l'affirme pas de cette manière car les grecs de l'Antiquité refusent toute idée de la notion d'infini actuelle. Il énonce :
« Les nombres premiers sont plus nombreux que toute multitude de nombres premiers proposés. »
Sa démonstration va dans ce sens. Soit un nombre premier : 7 par exemple. Démontrons qu'il en existe un plus grand. Formons alors le produit des nombres premiers inférieurs ou égaux augmenté de 1, soit 2x3x5x7+1. Ce nombre n'est pas divisible par 2, ni par 3, 5 ou 7. Il est donc premier et plus grand que 7.
Ce raisonnement peut être reproduit avec tout nombre premier.
« Les nombres premiers sont plus nombreux que toute multitude de nombres premiers proposés. »
Sa démonstration va dans ce sens. Soit un nombre premier : 7 par exemple. Démontrons qu'il en existe un plus grand. Formons alors le produit des nombres premiers inférieurs ou égaux augmenté de 1, soit 2x3x5x7+1. Ce nombre n'est pas divisible par 2, ni par 3, 5 ou 7. Il est donc premier et plus grand que 7.
Ce raisonnement peut être reproduit avec tout nombre premier.
Il invente aussi un algorithme bien célèbre qui porte aujourd’hui le nom d’algorithme d’Euclide permettant de calculer le PGCD de deux nombres (vu en 3e). Algorithme qu'il utilise également pour donner une méthode permettant de vérifier que deux nombres sont premiers entre eux.
Son œuvre ne s’arrête pas aux "Eléments". Il énonce 94 propositions sur les figures dans « Data », il étudie des partages de constructions dans « Les divisions », il étudie les perspectives dans « Optique » et dans «Phénomène», il traite d’astronomie.
Si vous voulez en savoir plus, cliquez sur les liens suivants :
- CultureMath, un article complet et très illustré sur le savant.
- Mathix un article très intéressant et fort illustré
- TrigoFACILE une rubrique très complète sur le sujet
- math93 très complet aussi
- m@ths et tiques Les cinq polyèdres de Platon
- Bibliographie
Avec le compas, Euclide (vu par Raphaël)
L'histoire de l'algèbre
Histoire de l'algèbre
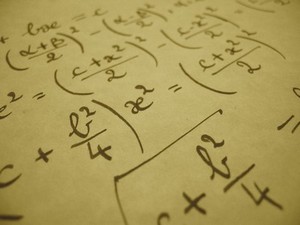
L’algèbre a d’abord été une branche des mathématiques qui concernait les règles des opérations sur les nombres et la résolution des équations pour devenir plus tard une théorie des opérations puis des propriétés sur les êtres mathématiques en général.
Cette rubrique tente de retracer la longue épopée d'une discipline qui a commencé, il y a plus de 4000 ans, à l’époque de la civilisation babylonienne et qui aujourd’hui encore poursuit son évolution...
Les initiateurs de l’algèbre :
La naissance de l'algèbre dans le monde arabo-musulman :
- al Khwarizmi et l’al jabr
- Abu Kamil
- Les algébristes arithméticiens
- Les géomètres algébristes
- Abu Kamil
- Les algébristes arithméticiens
- Les géomètres algébristes
L’algèbre dans le monde de l’Occident :
Les initiateurs de l’algèbre
Deux mille ans avant J.C., babyloniens et égyptiens savent résoudre de façon rhétorique des problèmes concrets du premier et second degré en utilisant implicitement des propriétés sur les opérations sans aucune notation symbolique. Les égyptiens possèdent toutefois quelques symboles comme ceux qui représentent l’addition (une paire de jambes marchant vers la gauche, le sens de l’écriture) et la soustraction (une paire de jambes marchant vers la droite).
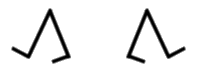
+ et -
Les calculateurs babyloniens désignent l’inconnue par "le côté" et la puissance deux est appelée "le carré".
Extrait d’un papyrus égyptien du 2e millénaire avant J.C.
Il y a un peu plus de 2000 ans, les chinois connaissaient des méthodes pour résoudre les systèmes linéaires proches de notre méthode des combinaisons linéaires. Ils employaient également la méthode de fausse position.
Extrait du manuscrit chinois « Neuf chapitres sur l’art du calcul », Ier siècle
2x = 1 + y
3y = 1 + z
4z = 1+ x
x, y et z étant les poids respectifs d’une gerbe de chaque récolte.
Extrait du Livre II Proposition 11 des Eléments d’Euclide.
Dans le langage d’aujourd’hui :
Soit [AB] un segment donné, il s’agit de déterminer le point H de [AB] tel que
le carré construit sur [AH] ait la même aire que le rectangle de côtés [HB] et [AB].
Ce qui revient à résoudre l’équation : x2 = AB(AB - x), où x = AH.
L’amorce du symbolisme en algèbre voit le jour dans « Les arithmétiques » avec Diophante d’Alexandrie (IIIe siècle) qui introduit un certain nombre d’abréviations. Les raisonnements restent cependant écrits en toute lettre. Sa notation est dite syncopée, ce qui signifie que les mots sont remplacés par des abréviations. Diophante utilise des techniques algébriques sans faire référence à la géométrie et par là, il s’oppose radicalement aux méthodes passées des géomètres grecs.
En Inde Chez Aryabhata l'Ancien (476 ; 550), on trouve dans son « Aryabhatîya », écrit en sanscrit en 510, des problèmes énoncés de façon concrète qui correspondent à des équations linéaires ou à des systèmes d’équations du premier degré.
Plus tard, dans le « Brahma Sphuta Siddhanta » (L’ouverture de l’Univers), datant de 628, Brahmagupta (598 ; 660) exprime des solutions d’équations quadratiques.
Problème donné par Aryabhata l'Ancien (476 ; 550)
Dans le langage d’aujourd’hui :
Si a et b sont les sommes possédées, c et d le nombre d’objets possédés, alors :
x = (b-a)/(c-d) est le prix de chaque objet.
La naissance de l’algèbre dans le monde arabo-musulman
Le développement de l’algèbre dans le monde arabo-musulman s’est effectué en deux temps.
Au VIIe et VIIIe siècle, les mathématiciens héritent du savoir passé (grec, indien, …) et entre dans une longue période de traduction.
Puis à partir du IXe siècle, de nouveaux travaux voient le jour.
Au VIIe et VIIIe siècle, les mathématiciens héritent du savoir passé (grec, indien, …) et entre dans une longue période de traduction.
Puis à partir du IXe siècle, de nouveaux travaux voient le jour.
Al Khwarizmi et l'al jabr :
Selon l’historien Ahmed Djebbar, l’acte de naissance officiel de l’algèbre en tant que discipline vient avec le savant perse Muhammad ibn Musa al-Khwarizmi (790 ; 850).
Dans un premier ouvrage, il expose le système décimal et les règles du calcul indien. Avec le « Kitâb al-jabr wa al-muqâbala » (Le livre du rajout et de l'équilibre), rédigé entre 813 et 833 et dédié au calife al Mamum, al Khwarizmi pose les bases des méthodes algébriques de résolution des équations ainsi qu’une synthèse des règles héritées des grecs et des textes néo-persans. En grande partie, l’ouvrage traite de problèmes de la vie courante (partages d’héritage, droits de succession, échanges commerciaux, arpentages des terres…) |  Al Khwarizmi |
Extrait du livre du rajout et de l'équilibre d'al Khwarizmi
Son algèbre reste rhétorique sans symbolisme aucun, même pour les nombres. Il appelle « dirham » (monnaie de l’époque) un nombre simple, « chay » (chose) l’inconnue et « mal » le carré de l’inconnue. Tous les coefficients sont positifs et tous les termes s’additionnent.
Sa technique consiste à ramener toutes les équations à l’une des six équations canoniques dont il sait trouver la solution :
Sa technique consiste à ramener toutes les équations à l’une des six équations canoniques dont il sait trouver la solution :
 |
1) ax2 = bx
2) ax2 = c 3) bx = c 4) ax2 + bx = c 5) ax2 + c = bx 6) bx + c = ax2 |
Pour y arriver, il utilise des méthodes de résolutions :
- al jabr (le reboutement, 4x - 3 = 5 devient 4x = 5 + 3). Dans l’équation, un terme négatif est accepté mais al Khwarizmi s’attache a s’en débarrasser au plus vite. Pour cela, il ajoute son opposé des deux côtés de l’équation.
Le mot "al jabr" est réutilisé dans de nombreux manuels antérieurs et deviendra en Europe : l’algèbre.
- al muqabala (la réduction, 4x = 9 + 3x devient x = 9)
Les termes semblables sont réduits.
- al hatt (2x = 8 devient x = 4)
Division de chaque terme par un même nombre.
Al Khwarizmi peut être considéré comme le fondateur d’une véritable théorie de résolution des équations quadratiques.
Il propose également quelques problèmes d’héritages menant à des systèmes d’équations mais qu’il ramène, pour les résoudre, à une équation linéaire. |  L'Algèbre d'Al Khwarizmi |
Abu Kamil :
Shuja Abu Kamil (850 ; 930) prolonge les travaux d’al Khwarizmi sur les équations quadratiques dans « al Kitab al kamil fi l-jabr wa l-muqabala » (Livre complet en algèbre).
Son second livre « Kita bat-tara’if l-hisab (Livre des choses rares en calcul) est entièrement consacré aux systèmes d’équations. Abu Kamil possède un degré d’abstraction supérieur à son prédécesseur.
Plus tard, Thabit ibn Qurra (836 ; 901) sera le premier à distinguer clairement les méthodes algébriques et géométriques et prouvera qu’elles mènent toutes les deux à la même solution.
|  Livre des choses rares d'Abu Kamil |
Extrait du Livre complet d'Abu Kamil
Le problème revient aujourd’hui à résoudre l’équation :
où x est le nombre de jours travaillés
6x = 4(30 - x)
Il faudra ensuite distinguer deux courants dans le monde arabe :
- les algébristes arithméticiens qui voient l’arithmétique au service de l’algèbre au moyen d’algorithmes numériques performants aidant à la résolution des équations. Abu Bakr al Karaji (953 ; 1029), au travers de son traité « al Kitab al fakhri fi l-jabr wa l-muqabala » (Le Fakhri en algèbre) en sera un acteur et fera progresser les méthodes sous l’influence des techniques algébriques des « Arithmétiques » de Diophante. Ses méthodes de calculs algébriques sur l'inconnue et ses différentes puissances donneront naissance à la théorie des polynômes.
A cette occasion, al Karaji expose un triangle de détermination du binôme (a+b)n.
- les algébristes arithméticiens qui voient l’arithmétique au service de l’algèbre au moyen d’algorithmes numériques performants aidant à la résolution des équations. Abu Bakr al Karaji (953 ; 1029), au travers de son traité « al Kitab al fakhri fi l-jabr wa l-muqabala » (Le Fakhri en algèbre) en sera un acteur et fera progresser les méthodes sous l’influence des techniques algébriques des « Arithmétiques » de Diophante. Ses méthodes de calculs algébriques sur l'inconnue et ses différentes puissances donneront naissance à la théorie des polynômes.
A cette occasion, al Karaji expose un triangle de détermination du binôme (a+b)n.
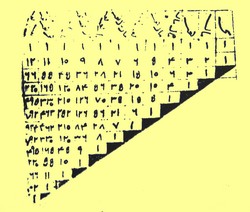
Triangle d'al Karaji
- les géomètres algébristes font avancer l’algèbre par la géométrie en étudiant en particulier les constructions géométriques permettant de représenter les racines des équations. Muhammad al Mahani (820 ; 880) s’intéresse au problème d’Archimède de Syracuse (-287 ; -212) exposé dans le traité « Sur la sphère et le cylindre » (Proposition 4 du Livre II). Ce problème consiste à étudier l’intersection d’une sphère par un plan. Il sera amené à résoudre par radicaux une équation du 3e degré du type x3 + r = px2, ce que les algébristes arithméticiens n’avaient pas encore tenté. Toutefois ses recherches resteront vaines.
D’autres mathématiciens du Xe siècle comme Abu Jafar al Khazin (900 ; 971) et al Hasan Ibn al Haytham (965 ; 1040), plus connu sous le nom d’Alhazen en Europe, reprennent des problèmes venus de l’Antiquité comme la duplication du cube, la trisection de l’angle ou certaines constructions de polygones qui mènent à des équations du 3e degré.
Plus tard, le mathématicien et poète Omar Khayyam (1048 ; 1123) écrit un traité sur les équations cubiques « Kitab a l-jabr wa l-muqabala » (Livre d’algèbre). Il dissocie l’algèbre de l’arithmétique et passe par les radicaux pour résoudre les équations. En utilisant les méthodes numériques ou géométriques, Omar Khayyam étudie les équations sous forme rhétorique mais dans des cas généraux : les coefficients sont des nombres positifs quelconques. Il remarque que les équations du 3e degré possèdent deux racines distinctes positives mais passe à côté de la troisième.
« Puisque tu ignores ce que te réserve demain, efforce-toi d'être heureux aujourd'hui. Prends une urne de vin, va t'asseoir au clair de lune, et bois, en te disant que la lune te cherchera peut être vainement, demain. » Extrait de Robaiyat, Omar Khayyam.
En 1170, dans « Les équations », Sharaf al Din al Tusi (1135 ; 1213) reprend les travaux des deux courants. Il passe par des discussions sur l’existence des racines positives en étudiant des courbes et en donnant des solutions numériques approximées. Son approche est locale et analytique. Cette conception sera poursuivie par Jemshid Al Kashi (1380 ; 1430) dans son « Traité de la corde et du sinus ». Il sera mené à donner une valeur approchée d’une équation du type x3 + q = px pour étudier le problème de la trisection de l’angle.
A partir du début du XVe siècle, les recherches mathématiques vont périclitées dans le monde arabe pour se propager en Europe en passant par l’Espagne musulmane.
L’algèbre en Occident
En Italie :
Tartaglia
Au XVe et XVIe siècle, l’algèbre prend son essor avec des méthodes de résolution pour des équations du 3e et 4e degré et l’apparition des nombres complexes. Les premières traductions de traités arabes comme le « Livre d’algèbre » d’al Khwarizmi ou le « Livre complet » d’Abu Kamil commencent à faire leur apparition.
L’Italie prend une certaine avance dans la réalisation de copies des ouvrages arabes. Celà s'explique par la constitution d’une grande classe de marchands ayant besoin de manuels de calcul.
L’Italie prend une certaine avance dans la réalisation de copies des ouvrages arabes. Celà s'explique par la constitution d’une grande classe de marchands ayant besoin de manuels de calcul.
Dans son « Liber Abaci », l’italien Léonard de Pise dit Fibonacci (1170 ; 1250) expose des éléments d’algèbre du passé qu’il enrichit de nouveaux problèmes et de nouvelles méthodes.
En 1494, dans « Summa de arithmetica, geometria, proporzioni et proporzionalita », Luca Pacioli (1445 ; 1517) donne une solution générale des équations du premier degré, sans notation exponentielle, mais avec de nombreuses abréviations. Il utilise par exemple les lettres p et m pour désigner respectivement une addition et une soustraction.
Lors d’un défi, l’italien Niccolo Fontana dit Tartaglia (1499 ; 1557) trouve la résolution générale d’équations du type x3 + px = q. Dans un premier temps, il ne voudra pas dévoiler sa formule jusqu’à ce que Gerolamo Cardano (1501 ; 1576), au nom francisé de Jérôme Cardan, lui arrache. C’est ce dernier qui, dans « Practica arithmeticae », admet sur des équations à cœfficients numériques des solutions négatives et manipule des racines carrées de nombres négatifs. En 1545, dans « Ars magne »,Cardan propose une méthode de résolution d’équations du 4e degré.
Résolution de l’équation du troisième degré donnée à Cardan en 1546, Tartaglia.
Rafaël Bombelli (1526 ; 1572) est premier à diffuser les problèmes de Diophante dans le monde de l’Occident. Comme Cardan, il étudie des équations de degrés supérieurs à 2 et considère les racines négatives.
Vers le symbolisme :
En 1484, Nicolas Chuquet (1445 ; 1500) écrit un remarquable ouvrage d’algèbre « Triparty en la science des nombres », mais son oeuvre n’est pas publiée et mal comprise de ses contemporains. Chuquet résout des systèmes d’équations du premier degré, utilise habilement les nombres négatifs jusqu’aux puissances négatives et établit des notations exponentielles. Par exemple, pour 12x3, il note 123.
En 1544, le moine allemand Michaël Stifel (1486 ; 1567) note l’inconnue par une sorte de r et travaille avec les nombres négatifs qu’il appelle nombre absurde.
Avec le français François Viète (1540 ; 1603), l’algèbre prend un nouveau tournant. Il conçoit l’écriture d’expressions à plusieurs inconnues et à coefficients littéraux. Ce qui permet d’apporter des méthodes de résolution dans des cas généraux. Il conserve une conception géométrique puisque les lettres représentent des grandeurs géométriques mais il n’hésite pas à dépasser la dimension 3 ce qui étonne Stifel qui qualifie sa vision de « contre-nature ». Viète peut être considéré comme le créateur du symbolisme mathématique moderne.
Avec René Descartes (1596 ; 1650), l’algèbre quitte sa forme syncopée et devient une branche totalement indépendante des mathématiques. C’est lui qui met en place les notations modernes que nous connaissons en algèbre, comme par exemple l’exposant pour les puissances.
Il propose d'utiliser les premières lettres de l'alphabet pour des quantités connues et les dernières pour les inconnues. Aujourd'hui encore, les paramètres sont habituellement notés a, b ou c alors que les variables sont x, y ou z. Grâce à un bon symbolisme, Descartes développe l’aspect « mécanique » du calcul algébrique qui, selon lui, permet de simplifier la pensée.
Utilisant ses récentes découvertes dans le domaine de la géométrie analytique, Descartes résout des équations du 3e et 4e degré en passant par la construction de courbes.
Il propose d'utiliser les premières lettres de l'alphabet pour des quantités connues et les dernières pour les inconnues. Aujourd'hui encore, les paramètres sont habituellement notés a, b ou c alors que les variables sont x, y ou z. Grâce à un bon symbolisme, Descartes développe l’aspect « mécanique » du calcul algébrique qui, selon lui, permet de simplifier la pensée.
Utilisant ses récentes découvertes dans le domaine de la géométrie analytique, Descartes résout des équations du 3e et 4e degré en passant par la construction de courbes.
Fin du XVIIe siècle, le symbole = entre dans l’écriture des équations. Ce symbole fut introduit en 1557 dans The Whetstone of Witte par l’anglais Robert Recorde (1510 ; 1558) : « Rien n’est plus pareil que deux lignes jumelles. »
Extrait de The Whetstone of Witte de Robert Recorde
Evolution moderne :
Au XVIIIe siècle, les progrès en algèbre se font plus rares avec les efforts donnés au calcul infinitésimal et le développement de l’analyse.
Alexandre Van der Monde (1735 ; 1796) travaille toutefois sur la résolution d’équations de degrés supérieurs. Et Joseph Lagrange (1736 ; 1813) puis Niels Abel (1802 ; 1829) s’attacheront à démontrer l’impossibilité de résoudre les équations du 5e degré avec des radicaux.
Le suisse Gabriel Cramer (1704 ; 1753) fait la première étude exhaustive des systèmes d’équations.
Alexandre Van der Monde (1735 ; 1796) travaille toutefois sur la résolution d’équations de degrés supérieurs. Et Joseph Lagrange (1736 ; 1813) puis Niels Abel (1802 ; 1829) s’attacheront à démontrer l’impossibilité de résoudre les équations du 5e degré avec des radicaux.
Le suisse Gabriel Cramer (1704 ; 1753) fait la première étude exhaustive des systèmes d’équations.
Au XIXe siècle, l’algèbre voit arriver les calculs de déterminants puis matriciels et d’autres mathématiciens tels Evariste Galois, ouvriront les portes de l’algèbre moderne … mais c’est là un autre sujet …
Pour finir, remontons le temps au travers d'une même "équation" :
Les équations produits
L'Histoire des "équations produits" remonte au temps des Grecs. Diophante (IVe siècle ap. J.-C.), d'origine syrienne vit à Alexandrie, en Egypte. Il a écrit de nombreux ouvrages, dont certains sont aujourd'hui perdus. Le plus célèbre s'appelle Arithmétique et traite de nombreux problèmes, résolus par des équations du premier et du second degré. Son oeuvre influencera de nombreux mathématiciens arabes, puis ceux des XVIe et XVIIe siècles, comme les français François Viète et Pierre de Fermat.
Maerten Van Heemskerck, le Phare d'Alexandrie, 1572.
Gravure de Filips Galle (1537-1612) d'après un dessin original.
Pierre de Fermat
« Passant, sous ce tombeau repose Diophante.
Ces quelques vers tracés par une main savante
Vont te faire connaître à quel âge il est mort.
Des jours assez nombreux que lui compta le sort,
Le sixième marqua le temps de son enfance ;
Le douzième fut pris par son adolescence.
Des sept parts de sa vie, une encore s'écoula,
Puis s'étant marié, sa femme lui donna
Cinq ans après un fils qui, du destin sévère
Reçut de jours hélas, deux fois moins que son père.
De quatre ans, dans les pleurs, celui-ci survécut.
Dis, tu sais compter, à quel âge il mourut. »
Extrait d’Eutrope publié en 369 dans "L'Abrégé de l'Histoire Romaine" traduit ici en alexandrins par Emile Fourrey (Récréations mathématiques, 1899).
Biographie de Diophante :
Diophante d'Alexandrie - Grec (IIIe siècle)Maerten Van Heemskerck, le Phare d'Alexandrie, 1572.
Gravure de Filips Galle (1537-1612) d'après un dessin original.
Probablement d’origine syrienne, Diophante passera l’essentiel de sa vie à Alexandrie.
Il est l’auteur de trois ouvrages de mathématiques dont un qui traite des nombres polygonaux et un second, disparu, appeléPorismes. Le plus célèbre, consacré à la résolution de problèmes s’appelle Les Arithmétiques.
Ce traité comprend treize livres mais seuls six d’entre eux étaient connus depuis le XVIe siècle. En 1972, la collection a pu s’enrichir de la découverte en Iran de quatre nouveaux tomes.
Cet ouvrage influencera grandement les savants arabes, auteurs de nombreuses traductions, comme celle du mathématicien perse Abu'l-Wafa. Les Arithmétiques est composé de 189 problèmes en grande partie résolus par des équations du premier et du second degré dont les solutions sont entières ou fractionnaires. Diophante considère comme absurde toute équation dont les racines ne sont pas rationnelles positives, contrairement à Archimède de Syracuse (-287 ; -212) ou encore Héron d’Alexandrie(Ier siècle) qui admettaient des solutions irrationnelles. Ils tentaient de s'en approcher en utilisant des conceptions géométriques.
Ce traité comprend treize livres mais seuls six d’entre eux étaient connus depuis le XVIe siècle. En 1972, la collection a pu s’enrichir de la découverte en Iran de quatre nouveaux tomes.
Cet ouvrage influencera grandement les savants arabes, auteurs de nombreuses traductions, comme celle du mathématicien perse Abu'l-Wafa. Les Arithmétiques est composé de 189 problèmes en grande partie résolus par des équations du premier et du second degré dont les solutions sont entières ou fractionnaires. Diophante considère comme absurde toute équation dont les racines ne sont pas rationnelles positives, contrairement à Archimède de Syracuse (-287 ; -212) ou encore Héron d’Alexandrie(Ier siècle) qui admettaient des solutions irrationnelles. Ils tentaient de s'en approcher en utilisant des conceptions géométriques.
Pierre de Fermat
Bien que les problèmes soient présentés de façon abstraite (« Trouver deux nombres tels que leurs somme et produit forment des nombres donnés »), leur résolution se fait numériquement sur des cas particuliers. Diophante utilise des techniques algébriques sans faire référence à la géométrie et par là, il s’oppose radicalement aux méthodes passées des géomètres grecs.
Les mathématiciens des XVIe et XVIIe siècles, tels François Viète (1540 ; 1603) et Pierre de Fermat (1601 ; 1665), le surnommeront, à juste titre, le « père de l’algèbre ».
En effet, Diophante n’hésite pas à introduire un « nombre indéterminé »,qu'il appelle l'arithme et que l’on peut assimiler aujourd’hui à l’inconnue utilisée en algèbre.
Il utilise des puissances d’exposant supérieur à 3 dont la représentation géométrique est impossible. Sa notation est ditesyncopée, ce qui signifie que les mots sont remplacés par des abréviations.
Il emploie des symboles pour les opérations. L’arithme est notée ζ, ou encore, ΔY pour x2 et KY pour x3.
Les mathématiciens des XVIe et XVIIe siècles, tels François Viète (1540 ; 1603) et Pierre de Fermat (1601 ; 1665), le surnommeront, à juste titre, le « père de l’algèbre ».
En effet, Diophante n’hésite pas à introduire un « nombre indéterminé »,qu'il appelle l'arithme et que l’on peut assimiler aujourd’hui à l’inconnue utilisée en algèbre.
Il utilise des puissances d’exposant supérieur à 3 dont la représentation géométrique est impossible. Sa notation est ditesyncopée, ce qui signifie que les mots sont remplacés par des abréviations.
Il emploie des symboles pour les opérations. L’arithme est notée ζ, ou encore, ΔY pour x2 et KY pour x3.
Par exemple, l'équation 4x2 + 3x = 10 se traduit rhétoriquement par "4 carrés joints à trois nombres font 10",
soit dans l'écriture de Diophante : ΔYδ ζγ εστι ι
soit dans l'écriture de Diophante : ΔYδ ζγ εστι ι
Diophante laisse son nom à une branche de l’algèbre, les équations diophantiennes. Ce sont des équations à plusieurs inconnues et à coefficients entiers ou rationnels qui mènent à un grand nombre de solutions entières ou rationnelles. Il existe de nombreux exemples d’équations diophantiennes dont la résolution se fait aujourd’hui à l’aide d’ordinateur :
- recherche de deux nombres entiers tels que la somme de leur carré soit un carré (triplets pythagoriciens)
- théorème de Bézout (voir le lien externe : homeomath)
- théorème de Fermat
- recherche de deux nombres entiers tels que la somme de leur carré soit un carré (triplets pythagoriciens)
- théorème de Bézout (voir le lien externe : homeomath)
- théorème de Fermat
En arithmétique, Diophante laisse encore un théorème élégant :
« Tout nombre premier de la forme 4n+1 est la somme de 2 carrés. »
« Tout nombre premier de la forme 4n+1 est la somme de 2 carrés. »
Bien que l’œuvre de Diophante fût mal comprise de ses contemporains, elle influença grandement les savants arabes et plus tard les mathématiciens occidentaux des XVIe et XVIIe siècles. Pierre de Fermat qui s’en inspire possède une traduction deClaude Gaspard Bachet de Méziriac (1581 ; 1638) devenue célèbre pour y avoir annoté qu’il détenait la démonstration de sa conjecture (voir La conjecture de Fermat).
Pour terminer voici l'épitaphe de Diophante donnant lieu à un exercice qui propose de calculer jusqu’à quel age vécut le savant :
Ces quelques vers tracés par une main savante
Vont te faire connaître à quel âge il est mort.
Des jours assez nombreux que lui compta le sort,
Le sixième marqua le temps de son enfance ;
Le douzième fut pris par son adolescence.
Des sept parts de sa vie, une encore s'écoula,
Puis s'étant marié, sa femme lui donna
Cinq ans après un fils qui, du destin sévère
Reçut de jours hélas, deux fois moins que son père.
De quatre ans, dans les pleurs, celui-ci survécut.
Dis, tu sais compter, à quel âge il mourut. »
Extrait d’Eutrope publié en 369 dans "L'Abrégé de l'Histoire Romaine" traduit ici en alexandrins par Emile Fourrey (Récréations mathématiques, 1899).
En mettant le problème en équation,
x = x/6 + x/12 + x/7 + 5 + x/2 + 4, soit : 84x/84 = 14x/84 + 7x/84 + 12x/84 + 420 + 42x/84 + 336 84x = 14x + 7x + 12x + 42x + 756 9x = 756 x = 84 Ainsi Diophante est mort à 84 ans. |
Euler
Euler a également eu un rôle dans l'histoire des fonctions. Voici sa biographie.
Leonhard Euler - Suisse (1707 ; 1783)
Johann Bernoulli
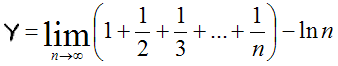
Leonhard Euler - Billet de 10 francs suisse
Alexis Clairaut
Leonhard Euler - Suisse (1707 ; 1783)
Cliquer sur l'image pour voir d'autres portraits
Leonhard Euler est issu d’une famille modeste vivant dans une ville près de Bâle en Suisse. Là, il suit des cours dans une école qui n’offre qu’un enseignement élémentaire et c’est son père qui l’initie aux premiers éléments des mathématiques. A 13 ans, il entre à l’Université de Bâle pour y étudier la philosophie et le droit. Il obtient son diplôme de philosophie à 16 ans mais son père qui souhaite le voir devenir pasteur, le pousse vers des études de théologie.
Très tôt, il devient l’élève de Johann Bernoulli (1667 ; 1748) un ami de son père, éminent mathématicien qui remarque son talent pour les maths.
Très tôt, il devient l’élève de Johann Bernoulli (1667 ; 1748) un ami de son père, éminent mathématicien qui remarque son talent pour les maths.
Johann Bernoulli
La suisse ne lui permettant pas de faire une carrière ambitieuse dans les sciences, il se voit appelé à Saint-Pétersbourg en 1727 par Catherine Ière, impératrice de Russie, sur la recommandation de Daniel (1700 ; 1782) et Nicolas Bernoulli (1687 ; 1759). En 1733, il succède à Daniel Bernoulli en qualité de professeur et à partir de 1740 il devient également responsable du département de géographie.
Euler rencontre la fille d’un artiste russe avec laquelle il aura 13 enfants dont seulement cinq survivront. Il est un père patient et attentionné. Euler raconte avoir fait ses plus belles découvertes avec un bébé dans ses bras et ses enfants jouant à ses pieds.
A 33 ans, il perd un oeil et bientôt il ne peut distinguer que de grands caractères tracés à la craie sur une ardoise.
En 1741, Frédéric II le Grand, roi de Prusse, le fait venir à Berlin pour rejoindre l’Académie de sciences. Mais il ne s’entend que moyennement avec ce dernier qui le surnomme le "Cyclope mathématique" en référence à son handicap. Il retourne à Saint-Pétersbourg en 1766, ville qu’il ne quittera plus.
A 33 ans, il perd un oeil et bientôt il ne peut distinguer que de grands caractères tracés à la craie sur une ardoise.
En 1741, Frédéric II le Grand, roi de Prusse, le fait venir à Berlin pour rejoindre l’Académie de sciences. Mais il ne s’entend que moyennement avec ce dernier qui le surnomme le "Cyclope mathématique" en référence à son handicap. Il retourne à Saint-Pétersbourg en 1766, ville qu’il ne quittera plus.
 |
Son activité restera constante jusqu’à la fin de sa vie.
Aidé par une mémoire phénoménale, il dicte ses textes à ses fils ou son valet, en ayant toujours le souci de la clarté dans ses écrits. En dépit de son handicap, Euler produira près de la moitié de son œuvre après 1765 en traitant de toutes les branches des mathématiques. Il meurt à Saint-Pétersbourg en 1783 alors âgé de 76 ans. Leonhard Euler |
En théorie des nombres, Euler démontre la conjecture de Fermat dans le cas n=3, étudie les nombres parfaits (nombre égal à la somme de ses diviseurs propres) et entretient des correspondances avec Christian Goldbach (1690 ; 1764), célèbre aujourd’hui pour sa conjecture.
Dans Introductio in analysin infinitorum (1748), il pose les fondements de l’analyse mathématique et de la mécanique analytique.Euler établit la célèbre constante, notée γ (gamma), qui porte aujourd’hui son nom : γ = 0,57721566490153286060…
Sa nature est un problème ouvert, on ne sait pas s’il s’agit d’un nombre rationnel ou irrationnel. Aujourd’hui près de 108 000 000 décimales de ce nombre sont connues. Le record est détenu par Patrick Demichel et Xavier Gourdon depuis 1999. La constante d’Euler, définit comme suit, demande quelques connaissances du lycée :
Sa nature est un problème ouvert, on ne sait pas s’il s’agit d’un nombre rationnel ou irrationnel. Aujourd’hui près de 108 000 000 décimales de ce nombre sont connues. Le record est détenu par Patrick Demichel et Xavier Gourdon depuis 1999. La constante d’Euler, définit comme suit, demande quelques connaissances du lycée :
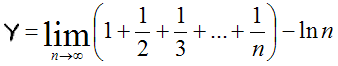
Euler fonde ce qu’on appelle aujourd’hui l’analyse fonctionnelle en donnant une définition précise de la notion de fonction. Nous lui devons la notation f(x) pour désigner l’image d’un nombre x par une fonction f.
Mais ce n’est de loin pas la seule notation qu’il introduit dans le langage des mathématiques. Il utilise la lettre grecque Σ comme symbole de sommation. Par exemple, 1 + 2 + 3 + … + 1000 trop long à écrire se note :
Mais ce n’est de loin pas la seule notation qu’il introduit dans le langage des mathématiques. Il utilise la lettre grecque Σ comme symbole de sommation. Par exemple, 1 + 2 + 3 + … + 1000 trop long à écrire se note :
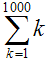
Il propose le célèbre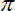 
pour le nombre Pi, la lettre i pour la racine carrée de -1 et le fameux e base des logarithmes népériens.
Il établit à ce sujet, une formule liant ces trois nombres : eiπ + 1 = 0 et une seconde mettant en relation la trigonométrie et l’analyse complexe : eix = cos x + i.sin x.
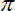pour le nombre Pi, la lettre i pour la racine carrée de -1 et le fameux e base des logarithmes népériens.Il établit à ce sujet, une formule liant ces trois nombres : eiπ + 1 = 0 et une seconde mettant en relation la trigonométrie et l’analyse complexe : eix = cos x + i.sin x.
Leonhard Euler - Billet de 10 francs suisse
Dans Institutiones calculi intégralis (1768/70), Euler développe également le calcul différentiel de Wilhelm Gottfried von Leibniz(1646 ; 1716) et la méthode des fluxions d’Isaac Newton (1642 ; 1727). Il prolonge les travaux des Bernoulli et met en place la notion d’équation aux dérivées partielles et le calcul des variations par la recherche des extrema sur les courbes.
En 1755, il publie Institutiones calculi differentialis, cum ejus usa in analysin infinitorum ac doctrinis serierum qui renferme ses recherches sur les séries.
Dans Vollständige Anleitung zur Algebra (Introduction complète à l’algèbre), publié en allemand en 1770, il présente ses travaux d’>algèbre élémentaire et démontre des théorèmes fondamentaux.
En 1755, il publie Institutiones calculi differentialis, cum ejus usa in analysin infinitorum ac doctrinis serierum qui renferme ses recherches sur les séries.
Dans Vollständige Anleitung zur Algebra (Introduction complète à l’algèbre), publié en allemand en 1770, il présente ses travaux d’>algèbre élémentaire et démontre des théorèmes fondamentaux.
En géométrie, il démontre une formule due à René Descartes (1596 ; 1650) et qui porte aujourd’hui son nom :
où S, F et A désignent respectivement le nombre de sommets, de faces et d'arêtes d’un polyèdre convexe.
|  |
La célèbre droite d’Euler (alignée sur le centre de gravité, le centre du cercle circonscrit et l’orthocentre d’un triangle) était un résultat déjà connu de Robert Simson (1687 ; 1768), mais le nom de ce dernier désigne une autre droite en relation avec le triangle.
Euler s’intéresse également à des problèmes d’astronomie tels que l’étude des orbites des planètes ou la trajectoire des comètes. Avec le mathématicien et astronome Alexis Clairaut (1713 ; 1765), il présente une théorie des mouvements de la lune.
Alexis Clairaut
Euler écrit aussi des ouvrages de physique : Mechanica, sive motus scientia, analytice exposita (1736), Theoria motus corporum solidorum seu rigidorum (1765). Il y définit le centre d’inertie, les moments d’inertie et les axes principaux d’inertie et traite sur la mécanique du point matériel. Il établie également des résultats dans de nombreux domaines tels que l’hydrodynamique, l’hydraulique, l’optique, l’élasticité, l’acoustique, la théorie des ondes lumineuses, …
Dans Lettres à une princesse d'Allemagne (la princesse d'Anhalt-Dessau, nièce du roi de Prusse), écrites de 1760 à 1762, Eulers'occupe de physique et de philosophie.
Dans Lettres à une princesse d'Allemagne (la princesse d'Anhalt-Dessau, nièce du roi de Prusse), écrites de 1760 à 1762, Eulers'occupe de physique et de philosophie.
Emmené par sa passion et son acharnement au travail, Euler nous laisse une œuvre gigantesque de 886 livres et articles qui abordent presque tous les domaines des mathématiques et des sciences en général.
Quelques sites supplémentaires sur sa biographie:
Inscription à :
Articles (Atom)